TRÒ CHƠI CỦA DIOPHANTUS
Trước tiên, tôi xin được làm rõ: đây là bài viết từ kỹ sư tin tặc Dương Ngọc Thái, và tôi đã nhờ nhà báo Đồng Phước Vinh biên tập lại để gửi đến các bạn.
Đây là câu chuyện về một trò chơi kéo dài 1.800 năm, bắt đầu từ một người Hy Lạp sống ở thế kỷ thứ hai tên là Diophantus. Sử sách không có nhiều thông tin về lai lịch của ông, chỉ biết rằng Diophantus thích làm toán, viết nhiều sách toán và một số cuốn còn lưu truyền đến nay.
Bí kíp thất lạc
Diophantus đặc biệt thích giải phương trình hai ẩn số. Nào ai ngờ, 18 thế kỷ sau, những bài toán Diophantus làm cho vui lại tạo thành cơ sở toán học cho những công nghệ bảo vệ mạng Internet.
Mỗi khi bạn gửi email, trò chuyện hay mua sắm qua Internet, thông tin của bạn được bảo vệ bởi những thuật toán mật mã dựa vào đường cong elliptic (Elliptic Curve Cryptography, từ đây viết tắt là ECC). ECC được phát minh vào cuối thế kỷ 20, nhưng có một sợi chỉ cho thấy mọi thứ khởi nguồn từ Diophantus.
Diophantus quan tâm đến những câu hỏi chẳng hạn như: Tìm các cặp số hữu tỉ (x, y) sao cho x2 + y2 = 1. Câu hỏi của Diophantus tương đương với tìm các điểm hữu tỉ trên đường tròn. Ngoài đường tròn, Diophantus muốn tìm điểm hữu tỉ trên nhiều loại đường cong.
Diophantus viết một bộ sách lừng danh mang tên Arithmetica (Số học), gồm 13 cuốn, để bàn về những câu hỏi như vậy.
Bộ sách Arithmetica được cất giữ ở thư viện Alexandria nhưng sau nhiều lần thư viện này bị đốt phá, bộ sách Arithmetica bị thất lạc. Arithmetica chính thức trở lại với dòng chảy toán học thế giới vào năm 1572, khi 143 bài toán của Diophantus bất ngờ xuất hiện trong cuốn “Algebra” của Bombelli, một giáo sư ở Đại học Bologna. Một người bạn của Bombelli đã phát hiện sáu cuốn Arithmetica trong thư viện Vatican.
Định lý cuối cùng
Sáu cuốn sách còn sót lại của Diophantus được dịch ra tiếng Latin lần đầu vào thế kỷ 16. Đến thế kỷ 17, một bản dịch của Bachet đến tay Fermat, để rồi vị luật sư người Pháp cũng làm toán cho vui đã khai sinh ra số học.
Chính bên lề cuốn Arithmetica của mình, Fermat đã viết những dòng chữ ám ảnh thế giới trong suốt hơn ba trăm năm:
Nhưng không thể nào chia một số mũ ba thành tổng hai số mũ ba, một số mũ bốn thành hai số mũ bốn, hoặc nói chung, đến vô cùng, bất kỳ số mũ nào cao hơn bình phương thành hai số mũ cùng bậc. Tôi đã tìm được một chứng minh kỳ diệu cho sự thật này, nhưng lề sách này chật quá không đủ chỗ để ghi lại.
Đây chính là phát biểu lừng danh Định lý cuối cùng của Fermat, được mệnh danh là con gà đẻ trứng vàng của toán học vì các nỗ lực chứng minh đã tạo ra nhiều loại toán mới.
Mặc dù thu hút sự chú ý của những bộ óc toán học vĩ đại nhất, định lý Fermat chỉ được Andrew Wiles và Richard Taylor chứng minh vào năm 1995. Điều thú vị là chứng minh của Wiles và Taylor lại dựa vào elliptic curve, vốn khởi nguồn từ Diophantus.
Như vậy chúng ta đã đi một vòng tròn, từ Diophantus đến Fermat, Wiles và Taylor để rồi quay lại Diophantus. Sợi dây liên kết tất cả chính là elliptic curve.
Những đường cong cong
Arithmetica chủ yếu bàn về những bài toán mà ngày nay chúng ta xem là đơn giản. Nhưng nếu đọc kỹ bạn sẽ thấy một bài toán rất khác so với phần còn lại: Bài toán số 24 trong cuốn số IV.
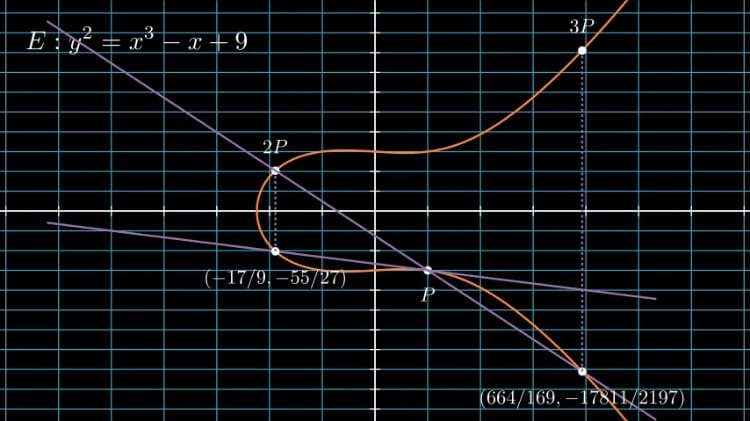
Trong bài toán này Diophantus muốn tìm các điểm hữu tỉ (x, y) thỏa mãn biểu thức y2 = x3 - x + 9. Ngày nay chúng ta biết biểu thức này biểu diễn một elliptic curve. Gọi đường cong này là E.
Dễ thấy sáu điểm nằm trên E: (0, 3), (0, -3), (1, 3), (1, -3), (-1, 3), (-1, -3). Câu hỏi của Diophantus vẫn là: còn điểm nào không?
Đây là một bài toán không đơn giản, ngay cả với tiêu chuẩn ngày nay. Nhưng, bằng một loạt các biến đổi tài tình, Diophantus tìm thêm được điểm (-17/9, -55/27).
Phải mất 1.500 năm người Trái Đất mới hiểu cơ sở toán học của những phép biến đổi mà Diophantus thực hiện để giải bài toán 24. Đến thế kỷ 17, Bachet và Fermat đưa ra công thức đại số để “nhân đôi” một điểm, còn Newton chỉ ra cơ sở hình học tuyệt đẹp của các phép biến đổi này.
Mặc dù Diophantus dừng lại khi tìm được điểm đầu tiên, phương pháp của ông ấy có thể giúp tìm được thêm vô số điểm khác.
Câu hỏi hiển nhiên tiếp theo là: phương pháp Diophantus có giúp tìm được tất cả điểm hữu tỉ hay không? Phải đến đầu những năm 1900, với sự dẫn dắt của Euler, Jacobi, Abel, Gauss, Poincare, Mordell, chúng ta mới trả lời được câu hỏi này.
Trong thế kỷ 20, lý thuyết elliptic curve trở thành đề tài nghiên cứu chính của toán học thế giới. Những nhánh chính của toán học như số học, đại số, hình học, giải tích gặp nhau ở elliptic curve, giao thoa tạo ra những kết quả rực rỡ.
Những gì Diophantus và bao nhà toán học theo đuổi trong hàng ngàn năm vì tò mò, bất ngờ tạo ra phương thức truyền thông an toàn, giúp cho Internet trở nên hữu ích và riêng tư hơn nhiều. Nền tảng an ninh của Bitcoin và nhiều loại tiền mã hóa cũng được xây dựng dựa trên elliptic curve.
Tại sao elliptic curve lại mang tên như vậy, trong khi nhìn không giống ellipse? Điều thú vị là câu trả lời lại có liên quan đến ông tổ ngành Big Data và quỹ đạo các hành tinh.
Ông tổ Big Data
Ngoài Arithmetica, thế kỷ 16 còn chứng kiến sự trở lại của thuyết nhật tâm (heliocentrism). Ngày nay chúng ta xem trái đất xoay quanh mặt trời là chuyện hiển nhiên, nhưng phải đến đầu thế kỷ 18, với sự đóng góp to lớn của Tycho, Kepler và Galileo, thuyết nhật tâm mới được chấp nhận.
Tycho Brahe là một nhà thiên văn học lỗi lạc người Đan Mạch. Năm 13 tuổi, Tycho chứng kiến nguyệt thực toàn phần ngày 21/8/1560 và rất thích thú khi biết hiện tượng này đã được dự báo trước nhưng bị trễ một ngày. Năm 16 tuổi, khi quan sát sự giao hội của sao Mộc và sao Thổ, Tycho một lần nữa lại thấy nhiều sai sót của dữ liệu quan trắc lúc bấy giờ.
Trong gần 40 năm tiếp theo, Tycho miệt mài quan sát và ghi nhận chi tiết sự chuyển động của các hành tinh, dành nhiều thời gian cải tiến công cụ và xây các đài thiên văn. Tycho thu thập được một bộ dữ liệu thiên văn chính xác gấp nhiều lần những bộ dữ liệu cùng thời cho đến trước khi kính viễn vọng ra đời vào đầu thế kỷ 17.
Có thể nói không ngoa, Tycho là nhà khoa học dữ liệu (data scientist) đầu tiên trong lịch sử, ông tổ của ngành Big Data.
Quỹ đạo hành tinh
Mặc dù bộ dữ liệu của Tycho rất giá trị, nhưng để hiểu dữ liệu đang nói gì thì cần thêm một thiên tài khác: Kepler.
Kepler làm trợ lý cho Tycho. Tycho thấy quỹ đạo sao Hỏa chệch khỏi dự đoán của các mô hình lúc bấy giờ, nên giao Kepler nhiệm vụ phân tích dữ liệu sao Hỏa.
Công việc của Kepler gặp nhiều khó khăn vì Tycho bảo vệ dữ liệu nghiêm ngặt, không cho phép Kepler sao chép. Chỉ đến khi Tycho bất ngờ qua đời vào năm 1601, Kepler mới tiếp cận được nguồn dữ liệu quý giá.
Từ dữ liệu Tycho để lại, Kepler đã phát hiện ba định luật lừng danh mang tên ông về chuyển động của các hành tinh. Định luật thứ nhất kết nối Kepler với Diophantus. Kepler phát hiện quỹ đạo các hành tinh không phải đường tròn, mà là đường ellipse.
Từ ellipse đến elliptic curve
Ellipse là một đường tròn biến dạng, dẹp hai đầu, giống hình oval. Nếu như đường tròn là tập hợp các điểm có cùng khoảng cách với tâm đường tròn, ellipse là tập hợp các điểm có cùng tổng khoảng cách đến hai tiêu điểm (foci).
Đường ellipse được biểu diễn bằng một biểu thức bậc hai, trong khi elliptic curve là biểu thức bậc ba. Khi chiếu lên không gian ba chiều, ellipse tương đương với quả bóng, còn elliptic curve tương đương với bánh xe máy.
Tuy nhiên, elliptic curve có tên nghe giống ellipse vì elliptic curve có liên quan đến bài toán tính chu vi ellipse. Muốn tính chu vi ellipse thì phải tính một tích phân gọi là elliptic integral loại thứ hai, nhưng chỉ có cách tính gần đúng elliptic integral, chứ không có công thức (closed form).
Mặc dù không tính được elliptic integral, nhưng vào thế kỷ 18, Fagnano và Euler phát hiện ra cách cộng elliptic integral. Nghĩa là nếu gọi elliptic integral là hàm f thì không ai tính được f(x) và f(y), nhưng lại có cách tính z, sao cho f(z) = f(x) + f(y). Quá lạ kỳ!
Đến thế kỷ 19, Jacobi cho thấy thuật toán cộng elliptic integral của Euler chính là phương pháp mà Diophantus đã dùng để giải phương trình y2 = x3 - x + 9. Từ đó, Jacobi, Abel và Gauss đề xuất đảo ngược elliptic integral, tập trung vào elliptic function, là những hàm phức có hai chu kỳ.
Để rồi sau đó Clebsch, Eisenstein và Weierstrass chỉ ra rằng vấn đề cần nghiên cứu cũng không phải là elliptic function, mà là những đường cong bậc ba xuất hiện một cách tự nhiên khi nghiên cứu tính chất của elliptic function. Họ gọi đó là elliptic curve.
Tóm lại: Tycho → Kepler → ellipse → elliptic integral → elliptic function → elliptic curve.
Vài dòng giới thiệu về tác giả Dương Ngọc Thái
Với vai trò Kỹ sư bảo mật tại Google, Dương Ngọc Thái đã có nhiều phát hiện ảnh hưởng lớn tới an toàn của internet toàn cầu. Công việc của anh Thái là giúp người dùng an toàn hơn khi sử dụng Gmail, Google Search, Android, YouTube và các sản phẩm khác của Google... Nổi tiếng nhất là bộ ba kỹ thuật tấn công mà anh Thái cùng cộng sự tạo ra mang tên BEAST, CRIME và POODLE. Nhiều năm anh là trưởng nhóm Bảo mật/Tiền mã hóa tại Google.
Bên cạnh đó, Anh Thái và nhóm của mình cũng đóng góp cho an toàn chung của mạng internet. Hai trong số những dự án này là Google Tink (thư viện mã nguồn mở đa nền tảng) và Project Wycheproof (công cụ kiểm tra điểm yếu của các thư viện mật mã). Hiện nay anh đã rời Google và mở một CT tư vấn tên Calif, và một trong những mục tiêu anh kể là hỗ trợ chống mã độc tấn công Việt Nam.
Các bạn có thể tham khảo bài viết đầy đủ của tác giả tại đây.
